파이썬 openCV 19번째 강의는 에지 검출 : 라플라시안(Laplacian), LoG(Laplacian of Gaussian), DoG(Difference of Gaussian)의 세 가지입니다. 라플라시안과 LoG는 라플라시안 필터를 사용한다는 공통점, LoG와 DoG는 Gaussian블러와 관련되어있다는 공통점으로 묶여있어 한번에 강의해보자 합니다.
0. 라플라시안(Laplacian), 가우시안(Gaussian)?
이번 강의에서 핵심적인 단어는 라플라시안과 가우시안입니다. 가우시안은 예전 가우시안 필터 강의에서 언급한 적이 있습니다.
2020/11/22 - [파이썬/openCV] - 파이썬 openCV 10. 가우시안 노이즈(Gaussian Noise)
파이썬 openCV 10. 가우시안 노이즈(Gaussian Noise)
파이썬 openCV 10번째 강의는 가우시안 노이즈(Gaussian Noise)입니다. 이번 강의에서는 가우시안 노이즈를 생성하는 방법과, 이미지 평균 연산을 통한 가우시안 노이즈 제거 방법을 동시에 알려드리
marisara.tistory.com
라플라시안 역시 가우시안과 마찬가지로 라플라스 연산을 적용한 필터라서 라플라시안 기법입니다.


실제 프로그램이 위와 같은 공식을 적용하여 화소를 연산하지는 않습니다. 다만 라플라시안 필터도 원래는 위와 같은 공식을 통해 유도할 수 있다고만 알아두시면 될 것 같습니다.

라플라스 연산자는 2차 미분을 할 때 필요한 연산자입니다. 저번 강의에서 사용했던 로버츠, 프리윗, 소벨은 1차 미분으로, 에지 유형에서 기울기에 따라 에지가 결정되었습니다. 하지만 라플라시안 필터는 2차 미분, 즉 기울기의 기울기 값으로, 조금 더 정확한 에지를 검출하기 위해 사용됩니다.
1. openCV에서의 라플라시안(Laplacian), LoG(Laplacian of Gaussian), DoG(Difference of Gaussian)
이제 각각의 코드를 확인해 보겠습니다.
img = cv2.imread('lenna.png')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
height, width = gray.shape우선 에지 검출의 공통적인 부분을 입력해줍니다
mask1 = np.array([[0, -1, 0], [-1, 4, -1], [0, -1, 0]])
mask2 = np.array([[1, 1, 1], [1, -8, 1], [1, 1, 1]])
mask3 = np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]])라플라시안 필터를 적용하기 위한 마스크를 생성해 줍니다.
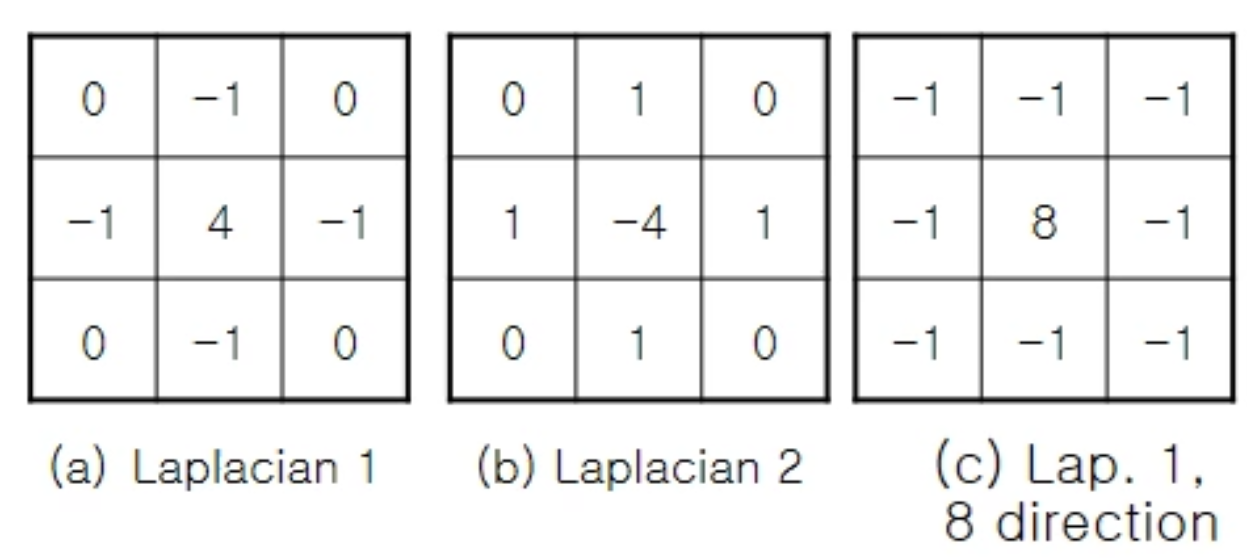
위 마스크들은 모두 라플라스 연산자에서 도출하는 필터입니다. 따라서 저 필터를 적용하는 것으로 라플라스 연산자를 이용하는 것과 같은 효과를 얻을 수 있습니다.
laplacian1 = cv2.filter2D(gray, -1, mask1)
laplacian2 = cv2.filter2D(gray, -1, mask2)
laplacian3 = cv2.filter2D(gray, -1, mask3)
laplacian4 = cv2.Laplacian(gray, -1)이제 각각의 라플라시안 필터를 적용해 줍니다. 마지막의 Laplacian함수는 위 필터의 함수화 버전입니다. 이때 필터를 따로 지정해주지 않으면(Laplacian함수의 3번째 인수) 자동으로 라플라시안 1번 필터(-1과 4가 있는 필터)를 사용합니다.
이제 라플라시안 필터를 확인해 보겠습니다. 이때 함수 타입을 실수로 지정해주어야 합니다.





각각의 필터 모두 에지가 잘 검출된 것을 확인할 수 있습니다.
이번에는 LoG입니다.
LoG는 Laplacian of Gaussian인 만큼, 가우시안을 적용하고 라플라시안을 사용하는 필터입니다. 이때 가우시안은 예전에 배웠던 가우시안 노이즈가 아닌, 가우시안 블러를 의미합니다.
gaussian = cv2.GaussianBlur(gray, (5, 5), 0)
LoG = cv2.filter2D(gaussian, -1, mask3)가우시안 블러는 GaussianBlur함수를 통해 적용합니다. 이때 각각의 인수는 (적용할 이미지, 필터 크기, 알파 값)이며, 이때 알파 값이 커지면 커질수록 블러링이 강하게 적용됩니다.
이제 LoG를 확인해 보겠습니다.



LoG는 일반적인 라플라시안 기법과 다르게 더 굵은 에지를 확인할 수 있습니다.
DoG는 Difference of Gaussian의 이름처럼 가우시안 블러를 적용한 이미지의 차입니다. 이때 차이로 가장 적합한 값은 두 알파 값의 비가 1.6 : 1입니다.
gaussian1 = cv2.GaussianBlur(gray, (5, 5), 1.6)
gaussian2 = cv2.GaussianBlur(gray, (5, 5), 1)
DoG = np.zeros_like(gray)
for i in range(height):
for j in range(width):
DoG[i][j] = float(gaussian1[i][j]) - float(gaussian2[i][j])가우시안 1과 가우시안 2의 알파 값의 비를 1.6 : 1로 설정하고, 각각의 화소의 차이를 출력할 배열에 넣어줍니다. 이때 굳이 실수 값으로 넣을 필요는 없으나, 실수값으로 넣어주어야 오버플로우를 방지할 수 있습니다.
이제 결과를 확인해보겠습니다.




DoG는 LoG와 비슷한 결과가 나오는 것을 확인할 수 있습니다.
2. 마치며
LoG와 DoG는 한국 웹사이트에서는 찾아보기 힘들었습니다. 그래서 외국 쪽 사이트인 stack overflow나 openCV공식 문서에서 배우시는 분들이 많으실 겁니다. 이번 강의로 다른 분들도 쉽게 LoG와 DoG를 공부하실 수 있으면 좋겠습니다.
def laplacian():
img = cv2.imread('lenna.png')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
height, width = gray.shape
mask1 = np.array([[0, -1, 0], [-1, 4, -1], [0, -1, 0]])
mask2 = np.array([[1, 1, 1], [1, -8, 1], [1, 1, 1]])
mask3 = np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]])
laplacian1 = cv2.filter2D(gray, -1, mask1)
laplacian2 = cv2.filter2D(gray, -1, mask2)
laplacian3 = cv2.filter2D(gray, -1, mask3)
laplacian4 = cv2.Laplacian(gray, -1)
gaussian = cv2.GaussianBlur(gray, (5, 5), 0)
LoG = cv2.filter2D(gaussian, -1, mask3)
gaussian1 = cv2.GaussianBlur(gray, (5, 5), 1.6)
gaussian2 = cv2.GaussianBlur(gray, (5, 5), 1)
DoG = np.zeros_like(gray)
for i in range(height):
for j in range(width):
DoG[i][j] = float(gaussian1[i][j]) - float(gaussian2[i][j])
cv2.imshow('original', gray)
cv2.imshow('laplacian1', laplacian1.astype(np.float))
cv2.imshow('laplacian2', laplacian2.astype(np.float))
cv2.imshow('laplacian3', laplacian3.astype(np.float))
cv2.imshow('laplacian4', laplacian3.astype(np.float))
cv2.imshow('gaussian', gaussian)
cv2.imshow('LoG', LoG.astype(np.float))
cv2.imshow('gaussian1', gaussian1)
cv2.imshow('gaussian2', gaussian2)
cv2.imshow('DoG', DoG)
cv2.waitKey(0)
'파이썬 강의 > openCV' 카테고리의 다른 글
| 파이썬 openCV 21. 노이즈 제거 : 나가오-마츠야마 필터(Nagao-Matsuyama filter) (0) | 2020.12.13 |
|---|---|
| 파이썬 openCV 20. 노이즈 제거 : 쿠와하라 필터(Kuwahara filter) (0) | 2020.12.10 |
| 파이썬 openCV 18. 에지검출 : 로버츠(roberts), 프리윗(prewitt), 소벨(sobel) (0) | 2020.12.07 |
| 파이썬 openCV 17. 에지검출 : 유사 연산자(Homogeneity)와 차 연산자(Difference)기법 (1) | 2020.12.06 |
| 파이썬 openCV 16. RGB에서 YCbCr로(RGB to YCbCr) (4) | 2020.12.02 |